Tidy a(n) lm object

Tidy summarizes information about the components of a model. A model component might be a single term in a regression, a single hypothesis, a cluster, or a class. Exactly what tidy considers to be a model component varies across models but is usually self-evident. If a model has several distinct types of components, you will need to specify which components to return.

# S3 method for lm
tidy(x, conf.int = FALSE, conf.level = 0.95, ...)

Arguments

x

An lm object created by stats::lm().

conf.int

Logical indicating whether or not to include a confidence interval in the tidied output. Defaults to FALSE.

conf.level

The confidence level to use for the confidence interval if conf.int = TRUE. Must be strictly greater than 0 and less than 1. Defaults to 0.95, which corresponds to a 95 percent confidence interval.

...

Additional arguments. Not used. Needed to match generic signature only. Cautionary note: Misspelled arguments will be absorbed in ..., where they will be ignored. If the misspelled argument has a default value, the default value will be used. For example, if you pass conf.lvel = 0.9, all computation will proceed using conf.level = 0.95. Additionally, if you pass newdata = my_tibble to an augment() method that does not accept a newdata argument, it will use the default value for the data argument.

Details

If the linear model is an mlm object (multiple linear model), there is an additional column response. See tidy.mlm().

See also

tidy(), stats::summary.lm()

Other lm tidiers: augment.glm(), augment.lm(), glance.glm(), glance.lm(), glance.summary.lm(), glance.svyglm(), tidy.glm(), tidy.lm.beta(), tidy.mlm(), tidy.summary.lm()

Value

A tibble::tibble() with columns:

conf.high

Upper bound on the confidence interval for the estimate.

conf.low

Lower bound on the confidence interval for the estimate.

estimate

The estimated value of the regression term.

p.value

The two-sided p-value associated with the observed statistic.

statistic

The value of a T-statistic to use in a hypothesis that the regression term is non-zero.

std.error

The standard error of the regression term.

term

The name of the regression term.

Examples

library(ggplot2)
library(dplyr)

mod <- lm(mpg ~ wt + qsec, data = mtcars)

tidy(mod)
#> # A tibble: 3 × 5
#>   term        estimate std.error statistic  p.value
#>   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
#> 1 (Intercept)   19.7       5.25       3.76 7.65e- 4
#> 2 wt            -5.05      0.484    -10.4  2.52e-11
#> 3 qsec           0.929     0.265      3.51 1.50e- 3
glance(mod)
#> # A tibble: 1 × 12
#>   r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
#>       <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
#> 1     0.826         0.814  2.60      69.0 9.39e-12     2  -74.4  157.  163.
#> # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

# coefficient plot
d <- tidy(mod, conf.int = TRUE)

ggplot(d, aes(estimate, term, xmin = conf.low, xmax = conf.high, height = 0)) +
  geom_point() +
  geom_vline(xintercept = 0, lty = 4) +
  geom_errorbarh()

  
# aside: There are tidy() and glance() methods for lm.summary objects too. 
# this can be useful when you want to conserve memory by converting large lm 
# objects into their leaner summary.lm equivalents.
s <- summary(mod)
tidy(s, conf.int = TRUE)
#> # A tibble: 3 × 7
#>   term        estimate std.error statistic  p.value conf.low conf.high
#>   <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
#> 1 (Intercept)   19.7       5.25       3.76 7.65e- 4    9.00      30.5 
#> 2 wt            -5.05      0.484    -10.4  2.52e-11   -6.04      -4.06
#> 3 qsec           0.929     0.265      3.51 1.50e- 3    0.387      1.47
glance(s)
#> # A tibble: 1 × 8
#>   r.squared adj.r.squared sigma statistic  p.value    df df.residual  nobs
#>       <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>       <int> <dbl>
#> 1     0.826         0.814  2.60      69.0 9.39e-12     2          29    32

augment(mod)
#> # A tibble: 32 × 10
#>    .rownames    mpg    wt  qsec .fitted  .resid   .hat .sigma .cooksd .std.resid
#>    <chr>      <dbl> <dbl> <dbl>   <dbl>   <dbl>  <dbl>  <dbl>   <dbl>      <dbl>
#>  1 Mazda RX4   21    2.62  16.5    21.8 -0.815  0.0693   2.64 2.63e-3    -0.325 
#>  2 Mazda RX4…  21    2.88  17.0    21.0 -0.0482 0.0444   2.64 5.59e-6    -0.0190
#>  3 Datsun 710  22.8  2.32  18.6    25.3 -2.53   0.0607   2.60 2.17e-2    -1.00  
#>  4 Hornet 4 …  21.4  3.22  19.4    21.6 -0.181  0.0576   2.64 1.05e-4    -0.0716
#>  5 Hornet Sp…  18.7  3.44  17.0    18.2  0.504  0.0389   2.64 5.29e-4     0.198 
#>  6 Valiant     18.1  3.46  20.2    21.1 -2.97   0.0957   2.58 5.10e-2    -1.20  
#>  7 Duster 360  14.3  3.57  15.8    16.4 -2.14   0.0729   2.61 1.93e-2    -0.857 
#>  8 Merc 240D   24.4  3.19  20      22.2  2.17   0.0791   2.61 2.18e-2     0.872 
#>  9 Merc 230    22.8  3.15  22.9    25.1 -2.32   0.295    2.59 1.59e-1    -1.07  
#> 10 Merc 280    19.2  3.44  18.3    19.4 -0.185  0.0358   2.64 6.55e-5    -0.0728
#> # … with 22 more rows
augment(mod, mtcars, interval = "confidence")
#> # A tibble: 32 × 20
#>    .rownames     mpg   cyl  disp    hp  drat    wt  qsec    vs    am  gear  carb
#>    <chr>       <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#>  1 Mazda RX4    21       6  160    110  3.9   2.62  16.5     0     1     4     4
#>  2 Mazda RX4 …  21       6  160    110  3.9   2.88  17.0     0     1     4     4
#>  3 Datsun 710   22.8     4  108     93  3.85  2.32  18.6     1     1     4     1
#>  4 Hornet 4 D…  21.4     6  258    110  3.08  3.22  19.4     1     0     3     1
#>  5 Hornet Spo…  18.7     8  360    175  3.15  3.44  17.0     0     0     3     2
#>  6 Valiant      18.1     6  225    105  2.76  3.46  20.2     1     0     3     1
#>  7 Duster 360   14.3     8  360    245  3.21  3.57  15.8     0     0     3     4
#>  8 Merc 240D    24.4     4  147.    62  3.69  3.19  20       1     0     4     2
#>  9 Merc 230     22.8     4  141.    95  3.92  3.15  22.9     1     0     4     2
#> 10 Merc 280     19.2     6  168.   123  3.92  3.44  18.3     1     0     4     4
#> # … with 22 more rows, and 8 more variables: .fitted <dbl>, .lower <dbl>,
#> #   .upper <dbl>, .resid <dbl>, .hat <dbl>, .sigma <dbl>, .cooksd <dbl>,
#> #   .std.resid <dbl>

# predict on new data
newdata <- mtcars %>%
  head(6) %>%
  mutate(wt = wt + 1)
augment(mod, newdata = newdata)
#> # A tibble: 6 × 14
#>   .rownames      mpg   cyl  disp    hp  drat    wt  qsec    vs    am  gear  carb
#>   <chr>        <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 Mazda RX4     21       6   160   110  3.9   3.62  16.5     0     1     4     4
#> 2 Mazda RX4 W…  21       6   160   110  3.9   3.88  17.0     0     1     4     4
#> 3 Datsun 710    22.8     4   108    93  3.85  3.32  18.6     1     1     4     1
#> 4 Hornet 4 Dr…  21.4     6   258   110  3.08  4.22  19.4     1     0     3     1
#> 5 Hornet Spor…  18.7     8   360   175  3.15  4.44  17.0     0     0     3     2
#> 6 Valiant       18.1     6   225   105  2.76  4.46  20.2     1     0     3     1
#> # … with 2 more variables: .fitted <dbl>, .resid <dbl>

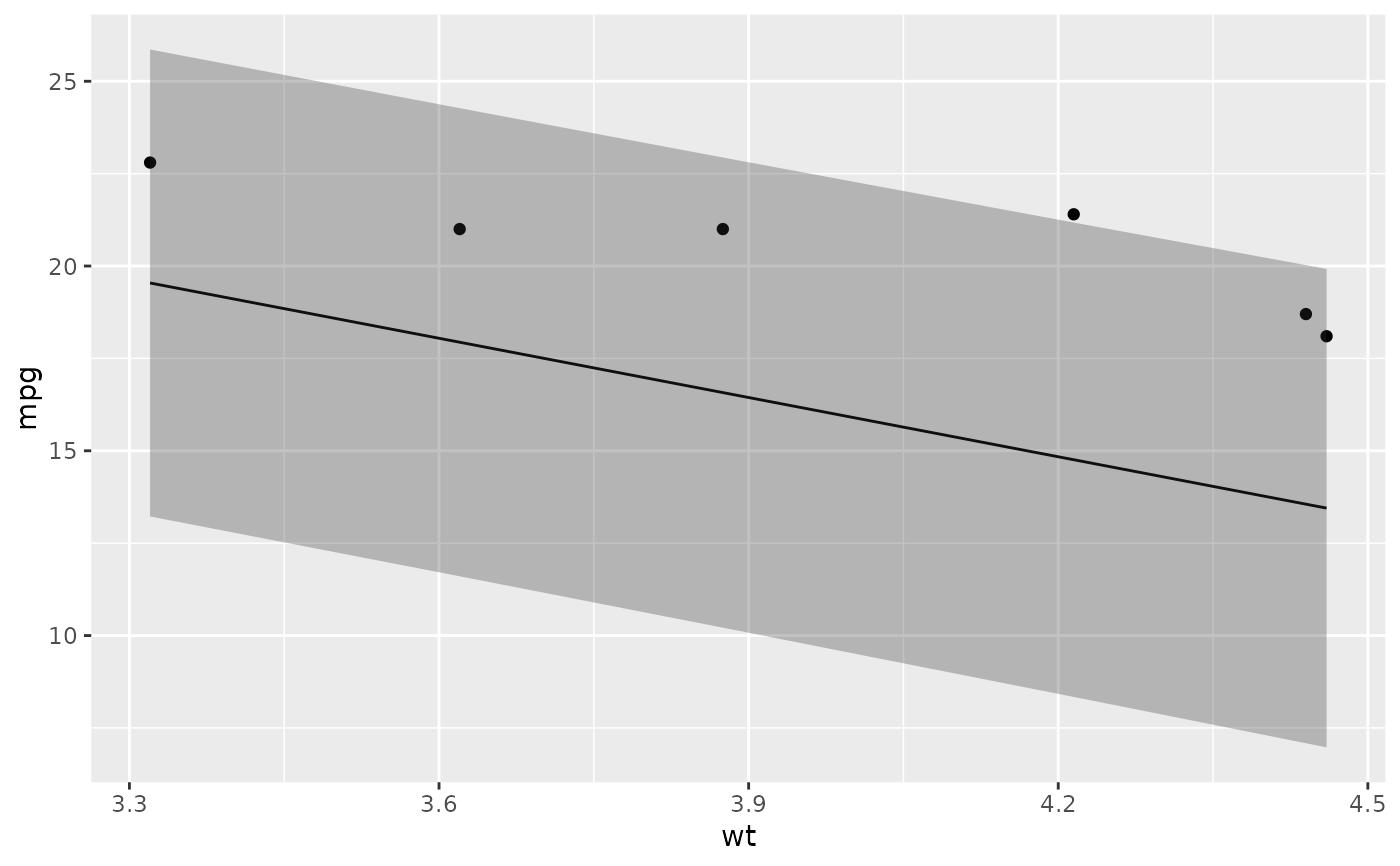
# ggplot2 example where we also construct 95% prediction interval

# simpler bivariate model since we're plotting in 2D
mod2 <- lm(mpg ~ wt, data = mtcars) 

au <- augment(mod2, newdata = newdata, interval = "prediction")

ggplot(au, aes(wt, mpg)) + 
  geom_point() +
  geom_line(aes(y = .fitted)) + 
  geom_ribbon(aes(ymin = .lower, ymax = .upper), col = NA, alpha = 0.3)


# predict on new data without outcome variable. Output does not include .resid
newdata <- newdata %>%
  select(-mpg)
  
augment(mod, newdata = newdata)
#> Warning: 'newdata' had 6 rows but variables found have 234 rows
#> # A tibble: 6 × 12
#>   .rownames    cyl  disp    hp  drat    wt  qsec    vs    am  gear  carb .fitted
#>   <chr>      <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>   <dbl>
#> 1 Mazda RX4      6   160   110  3.9   3.62  16.5     0     1     4     4    16.8
#> 2 Mazda RX4…     6   160   110  3.9   3.88  17.0     0     1     4     4    16.0
#> 3 Datsun 710     4   108    93  3.85  3.32  18.6     1     1     4     1    20.3
#> 4 Hornet 4 …     6   258   110  3.08  4.22  19.4     1     0     3     1    16.5
#> 5 Hornet Sp…     8   360   175  3.15  4.44  17.0     0     0     3     2    13.1
#> 6 Valiant        6   225   105  2.76  4.46  20.2     1     0     3     1    16.0

au <- augment(mod, data = mtcars)

ggplot(au, aes(.hat, .std.resid)) +
  geom_vline(size = 2, colour = "white", xintercept = 0) +
  geom_hline(size = 2, colour = "white", yintercept = 0) +
  geom_point() +
  geom_smooth(se = FALSE)
#> `geom_smooth()` using method = 'loess' and formula 'y ~ x'


plot(mod, which = 6)


ggplot(au, aes(.hat, .cooksd)) +
  geom_vline(xintercept = 0, colour = NA) +
  geom_abline(slope = seq(0, 3, by = 0.5), colour = "white") +
  geom_smooth(se = FALSE) +
  geom_point()
#> `geom_smooth()` using method = 'loess' and formula 'y ~ x'


# column-wise models
a <- matrix(rnorm(20), nrow = 10)
b <- a + rnorm(length(a))
result <- lm(b ~ a)

tidy(result)
#> # A tibble: 6 × 6
#>   response term        estimate std.error statistic p.value
#>   <chr>    <chr>          <dbl>     <dbl>     <dbl>   <dbl>
#> 1 Y1       (Intercept)  0.120       0.460    0.260  0.802  
#> 2 Y1       a1           1.40        0.400    3.51   0.00987
#> 3 Y1       a2           0.00979     0.337    0.0291 0.978  
#> 4 Y2       (Intercept) -0.300       0.320   -0.940  0.379  
#> 5 Y2       a1           0.160       0.278    0.578  0.582  
#> 6 Y2       a2           0.913       0.234    3.90   0.00589