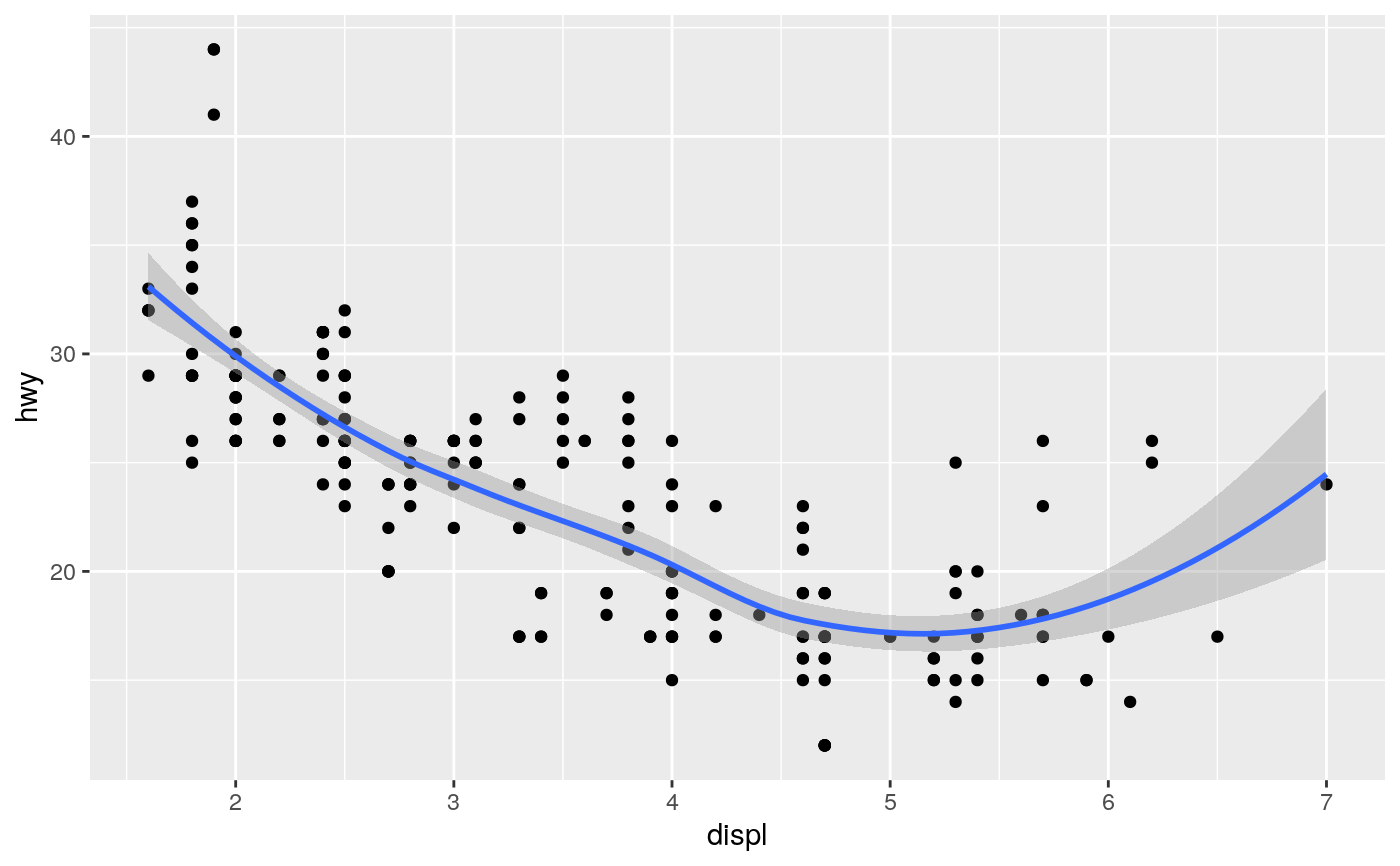
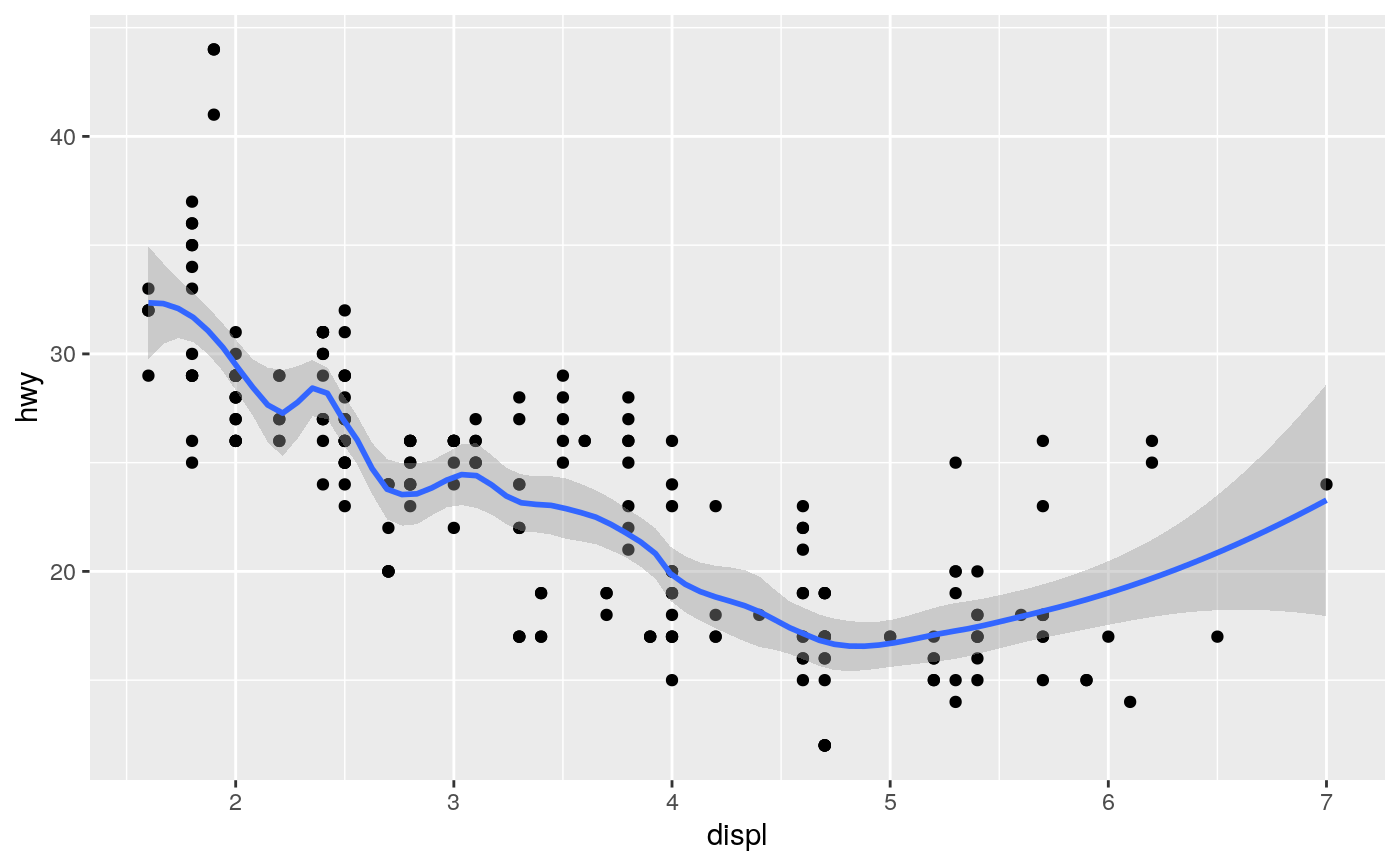
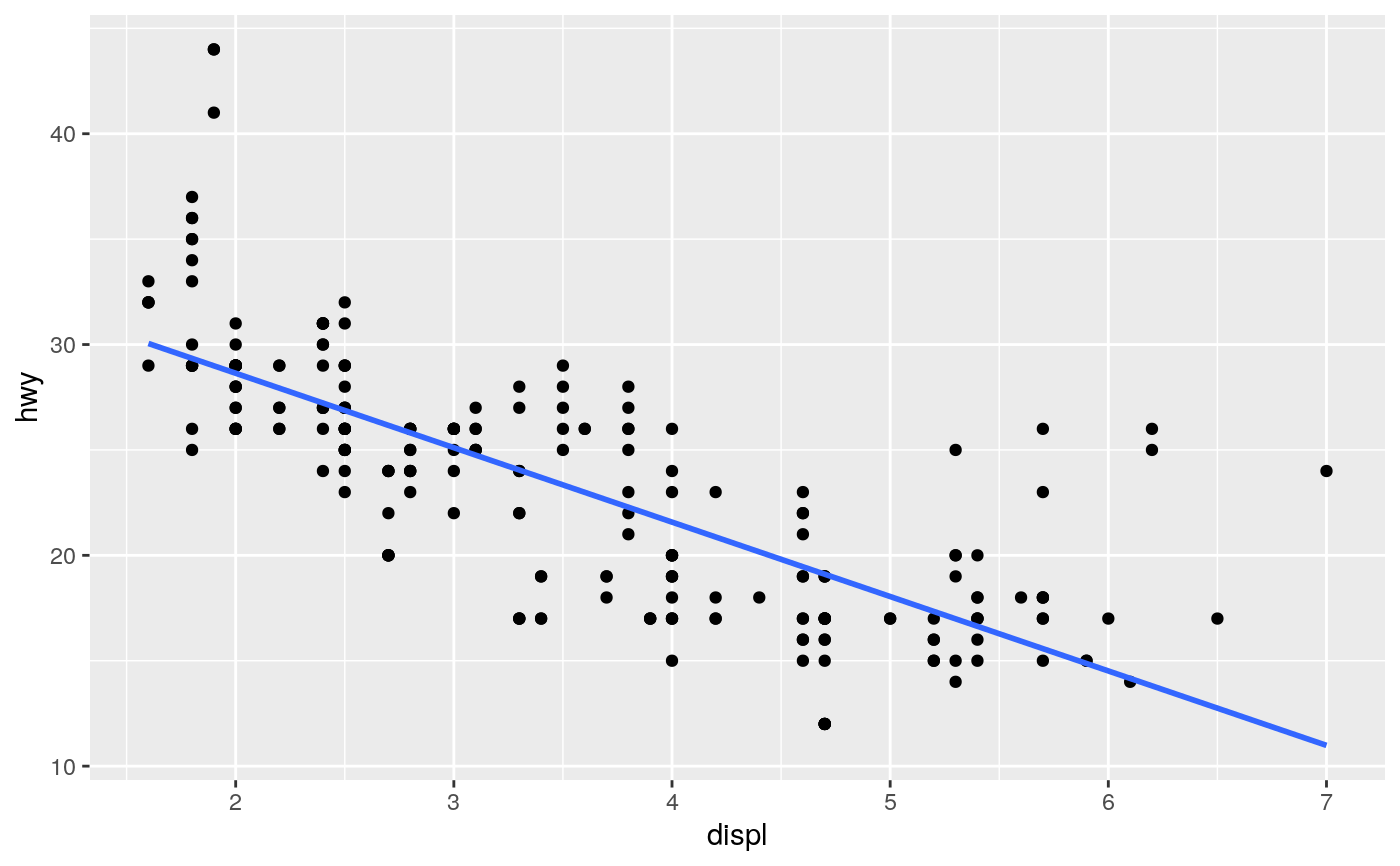
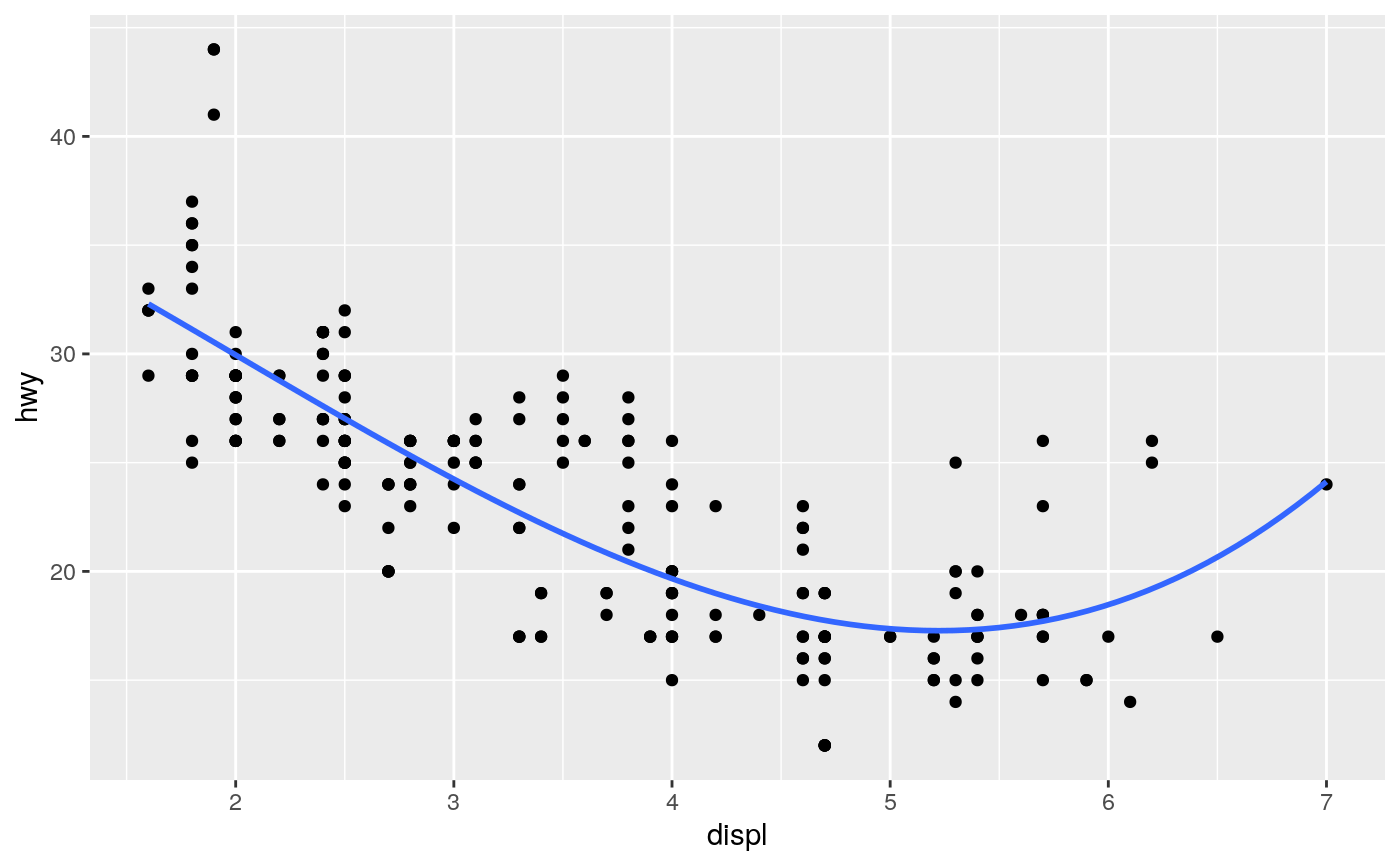
Aids the eye in seeing patterns in the presence of overplotting.
geom_smooth() and stat_smooth() are effectively aliases: they
both use the same arguments. Use stat_smooth() if you want to
display the results with a non-standard geom.
geom_smooth(mapping = NULL, data = NULL, stat = "smooth", position = "identity", ..., method = "auto", formula = y ~ x, se = TRUE, na.rm = FALSE, show.legend = NA, inherit.aes = TRUE) stat_smooth(mapping = NULL, data = NULL, geom = "smooth", position = "identity", ..., method = "auto", formula = y ~ x, se = TRUE, n = 80, span = 0.75, fullrange = FALSE, level = 0.95, method.args = list(), na.rm = FALSE, show.legend = NA, inherit.aes = TRUE)
Arguments
| mapping | Set of aesthetic mappings created by |
|---|---|
| data | The data to be displayed in this layer. There are three options: If A A |
| position | Position adjustment, either as a string, or the result of a call to a position adjustment function. |
| ... | Other arguments passed on to |
| method | Smoothing method (function) to use, accepts either a character vector,
e.g. For If you have fewer than 1,000 observations but want to use the same |
| formula | Formula to use in smoothing function, eg. |
| se | Display confidence interval around smooth? ( |
| na.rm | If |
| show.legend | logical. Should this layer be included in the legends?
|
| inherit.aes | If |
| geom, stat | Use to override the default connection between
|
| n | Number of points at which to evaluate smoother. |
| span | Controls the amount of smoothing for the default loess smoother. Smaller numbers produce wigglier lines, larger numbers produce smoother lines. |
| fullrange | Should the fit span the full range of the plot, or just the data? |
| level | Level of confidence interval to use (0.95 by default). |
| method.args | List of additional arguments passed on to the modelling
function defined by |
Details
Calculation is performed by the (currently undocumented)
predictdf() generic and its methods. For most methods the standard
error bounds are computed using the predict() method -- the
exceptions are loess(), which uses a t-based approximation, and
glm(), where the normal confidence interval is constructed on the link
scale and then back-transformed to the response scale.
Aesthetics
geom_smooth() understands the following aesthetics (required aesthetics are in bold):
xyalphacolourfillgrouplinetypesizeweightymaxymin
Learn more about setting these aesthetics in vignette("ggplot2-specs").
Computed variables
- y
predicted value
- ymin
lower pointwise confidence interval around the mean
- ymax
upper pointwise confidence interval around the mean
- se
standard error
See also
See individual modelling functions for more details:
lm() for linear smooths,
glm() for generalised linear smooths, and
loess() for local smooths.
Examples
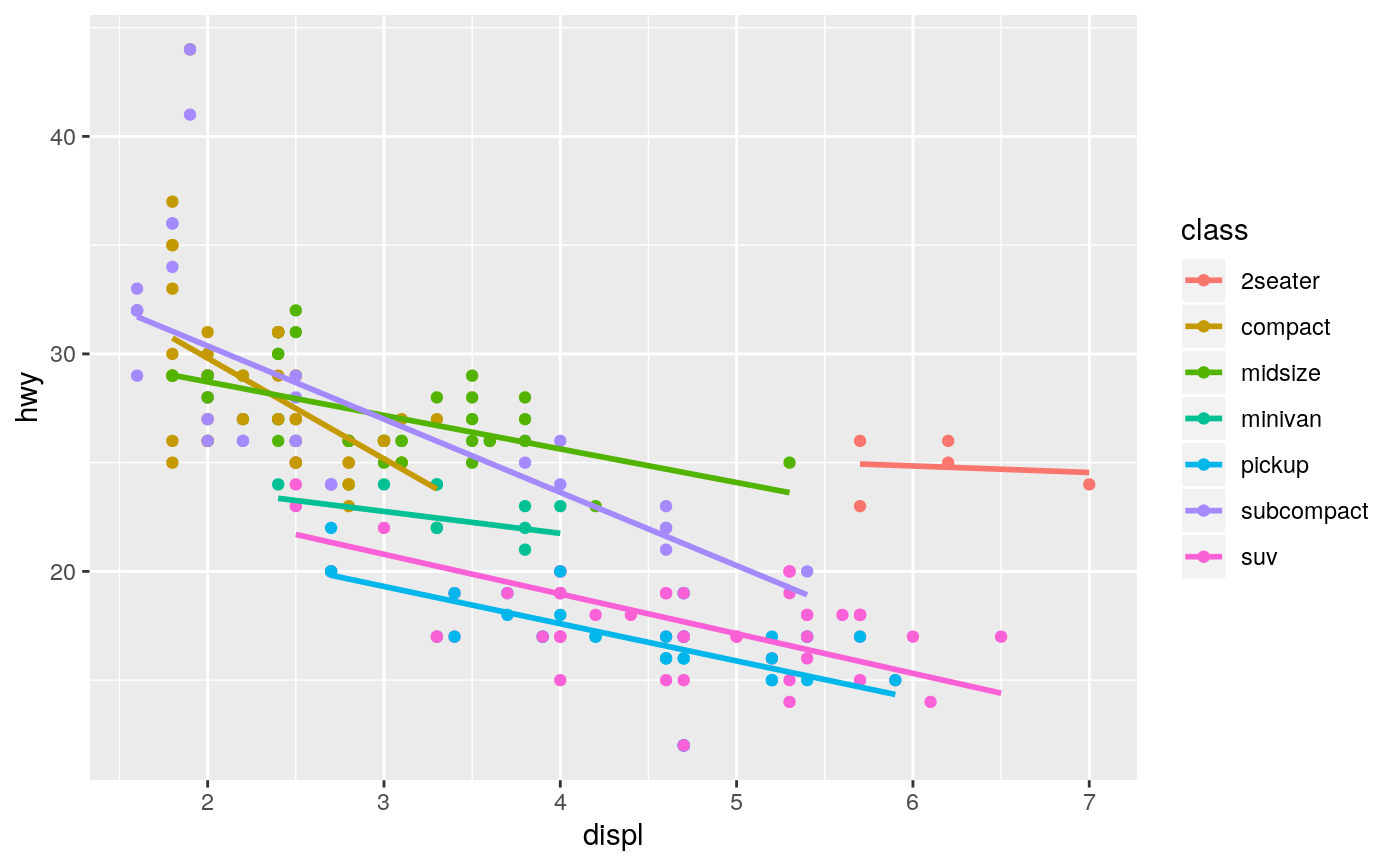
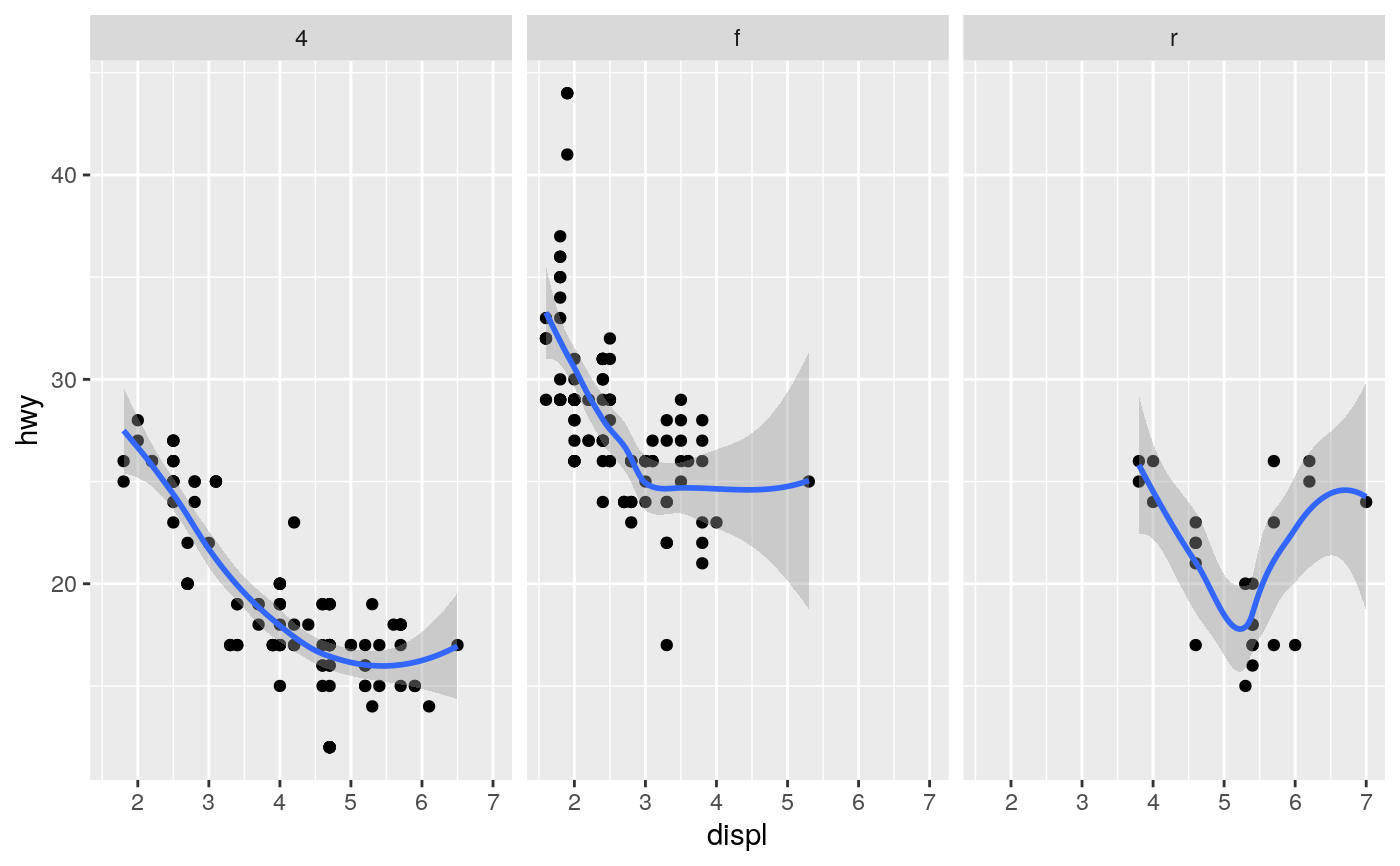
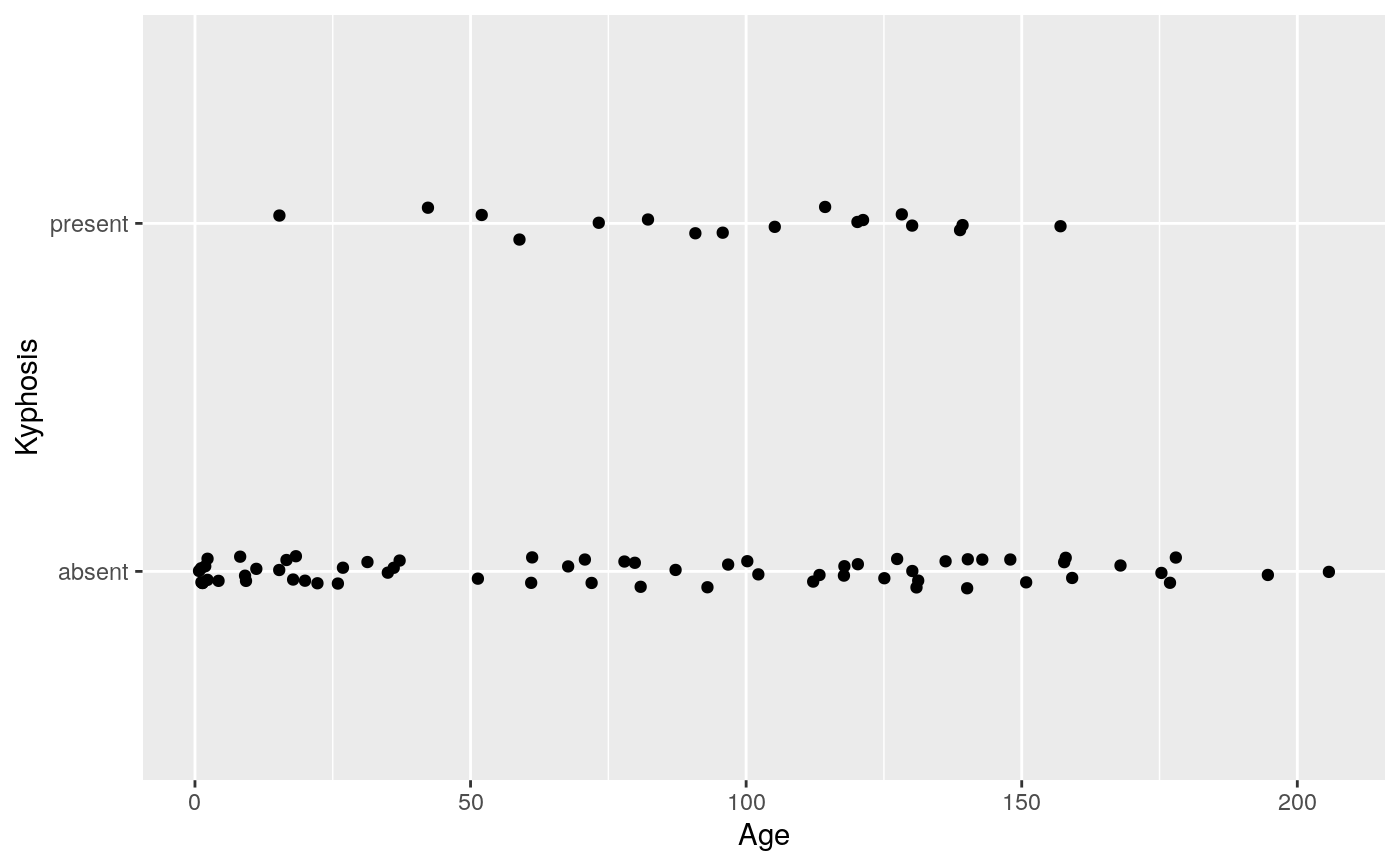
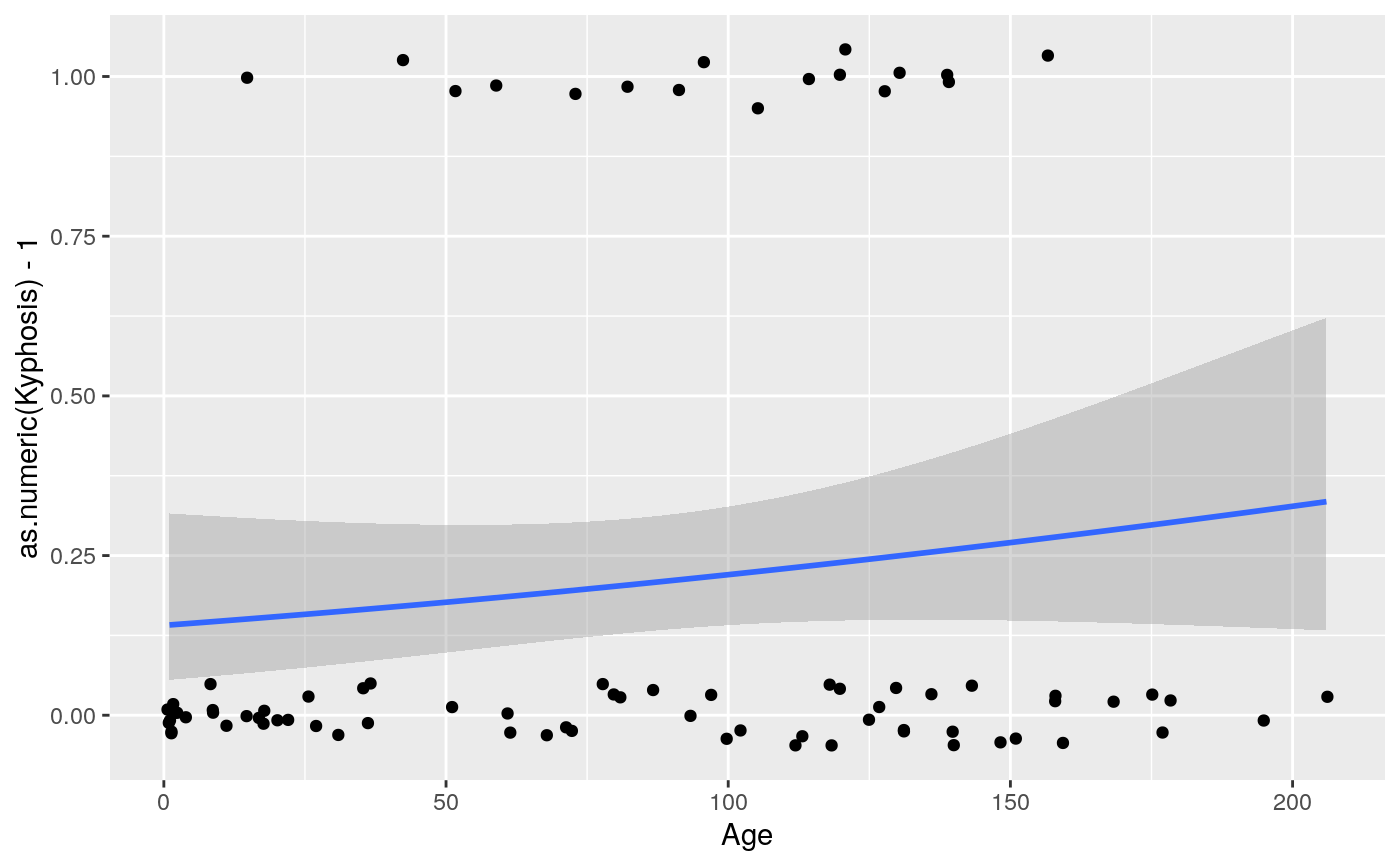
#># Use span to control the "wiggliness" of the default loess smoother. # The span is the fraction of points used to fit each local regression: # small numbers make a wigglier curve, larger numbers make a smoother curve. ggplot(mpg, aes(displ, hwy)) + geom_point() + geom_smooth(span = 0.3)#># Instead of a loess smooth, you can use any other modelling function: ggplot(mpg, aes(displ, hwy)) + geom_point() + geom_smooth(method = lm, se = FALSE)ggplot(mpg, aes(displ, hwy)) + geom_point() + geom_smooth(method = lm, formula = y ~ splines::bs(x, 3), se = FALSE)# Smooths are automatically fit to each group (defined by categorical # aesthetics or the group aesthetic) and for each facet. ggplot(mpg, aes(displ, hwy, colour = class)) + geom_point() + geom_smooth(se = FALSE, method = lm)#># \donttest{ binomial_smooth <- function(...) { geom_smooth(method = "glm", method.args = list(family = "binomial"), ...) } # To fit a logistic regression, you need to coerce the values to # a numeric vector lying between 0 and 1. ggplot(rpart::kyphosis, aes(Age, Kyphosis)) + geom_jitter(height = 0.05) + binomial_smooth()#> Warning: Computation failed in `stat_smooth()`: #> y values must be 0 <= y <= 1ggplot(rpart::kyphosis, aes(Age, as.numeric(Kyphosis) - 1)) + geom_jitter(height = 0.05) + binomial_smooth()ggplot(rpart::kyphosis, aes(Age, as.numeric(Kyphosis) - 1)) + geom_jitter(height = 0.05) + binomial_smooth(formula = y ~ splines::ns(x, 2))# But in this case, it's probably better to fit the model yourself # so you can exercise more control and see whether or not it's a good model. # }