This model is used in a lot of package tests, but it can be useful to support user experimentation as well.
house(...)Arguments
- ...
passed to
update().
Value
A packmod object, ready to simulate.
Examples
mod <- mrgsolve::house()
see(mod)
#>
#> Model file: housemodel.cpp
#> $PROB
#>
#> # `mrgsolve` housemodel
#>
#> This model is compiled with `mrgsolve`.
#>
#> - Author: Metrum Research Group, LLC
#> - Description: Generic indirect response PK/PD model
#> - Covariates: Weight, female sex
#> - Random effects: CL, VC, KA, KOUT
#> - Error model: exponential
#>
#>
#>
#> $PLUGIN base
#>
#> $PARAM @annotated
#> CL : 1 : Clearance (L/hr)
#> VC : 20 : Volume of distribution (L)
#> KA : 1.2 : Absorption rate constant (1/hr)
#> F1 : 1.0 : Bioavailability fraction (.)
#> D1 : 2.0 : Infusion duration (hr)
#> WT : 70 : Weight (kg)
#> SEX : 0 : Covariate female sex
#> WTCL : 0.75 : Exponent WT on CL
#> WTVC : 1.00 : Exponent WT on VC
#> SEXCL: 0.7 : Prop cov effect on CL
#> SEXVC: 0.85 : Prop cov effect on VC
#> KIN : 100 : Resp prod rate constant (1/hr)
#> KOUT : 2 : Resp elim rate constant (1/hr)
#> IC50 : 10 : Conc giving 50% max resp (ng/ml)
#>
#> $CMT @annotated
#> GUT : Dosing compartment (mg)
#> CENT : Central compartment (mg)
#> RESP : Response (unitless)
#>
#> $OMEGA @labels ECL EVC EKA EKOUT
#> 0 0 0 0
#>
#> $SIGMA @labels EXPO
#> 0
#>
#> $SET end=120, delta=0.25
#>
#>
#> $GLOBAL
#> #define CP (CENT/VCi)
#> #define INH (CP/(IC50+CP))
#>
#> typedef double localdouble;
#>
#> $MAIN
#> F_GUT = F1;
#> D_CENT = D1;
#>
#> double CLi = exp(log(CL) + WTCL*log(WT/70) + log(SEXCL)*SEX + ECL);
#> double VCi = exp(log(VC) + WTVC*log(WT/70) + log(SEXVC)*SEX + EVC);
#> double KAi = exp(log(KA) + EKA);
#> double KOUTi = exp(log(KOUT) + EKOUT);
#>
#> RESP_0 = KIN/KOUTi;
#>
#> $ODE
#> dxdt_GUT = -KAi*GUT;
#> dxdt_CENT = KAi*GUT - (CLi/VCi)*CENT;
#> dxdt_RESP = KIN*(1-INH) - KOUTi*RESP;
#>
#> $TABLE
#> double DV = CP*exp(EXPO);
#>
#> $CAPTURE @annotated
#> DV: Dependent variable (ng/ml)
#> CP: Plasma concentration (ng/ml)
#>
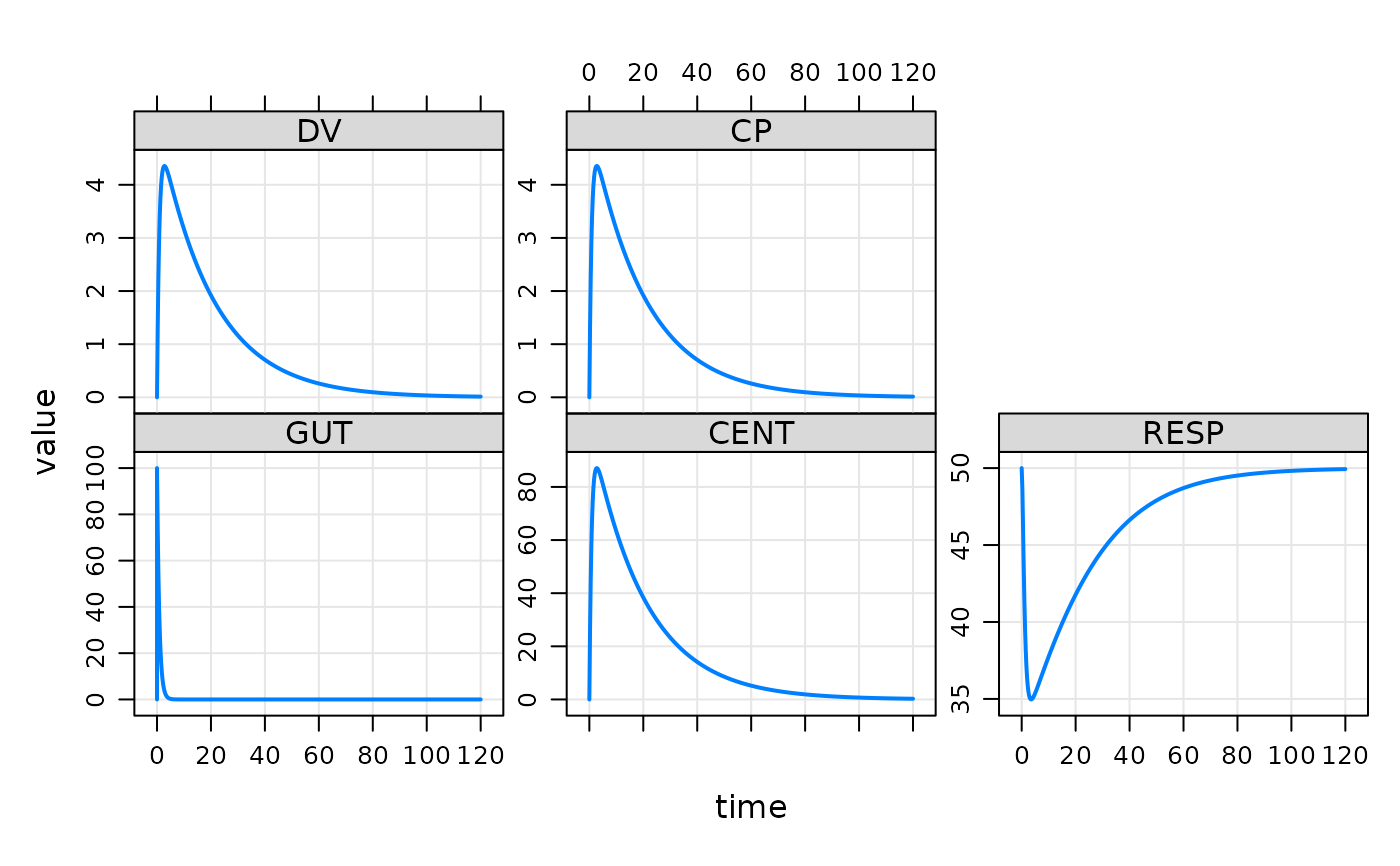
mod %>% ev(amt = 100) %>% mrgsim() %>% plot()